Análise Combinatória Resumo
Análise Combinatória, Resumo para você esudar para o ENEM.
Análise combinatória
A análise combinatória é um ramo da matemática que estuda técnicas de contagem e organização de diferentes maneiras de agrupar, organizar ou selecionar elementos de conjuntos finitos, sem considerar propriedades específicas desses elementos.
Ela abrange conceitos como permutações, combinações, arranjos e permutações com repetição, sendo amplamente aplicada em problemas de probabilidade, estatística, ciências da computação, entre outros.
Veja o que veremos aui:
| Índice: |
O que é Análise combinatória
A análise combinatória é uma área da matemática que lida com a contagem e organização de diferentes combinações e arranjos de elementos, sem necessariamente levar em conta as propriedades específicas desses elementos.
Em outras palavras, ela trata de quantas maneiras diferentes podemos organizar, selecionar ou agrupar elementos de um conjunto, levando em consideração as regras de contagem.
Existem várias técnicas dentro da análise combinatória para resolver diferentes tipos de problemas, incluindo:
1. Permutações:
Arranjos ordenados de elementos. Por exemplo, quantas maneiras diferentes podemos organizar as letras da palavra “ABACAXI”?
Veja mais sobre as permutações.
2. Combinações:
Seleções não ordenadas de elementos. Por exemplo, quantos grupos diferentes de 3 pessoas podemos formar a partir de um grupo de 6 pessoas?
Veja mais sobre as combinações.
3. Arranjos:
Arranjos ordenados de elementos, mas com restrições adicionais. Por exemplo, quantas maneiras diferentes podemos escolher 3 pratos de um menu de 5 pratos?
Veja mais sobre os arranjos.
4. Permutações com repetição:
Permutações de elementos onde alguns ou todos podem ser repetidos. Por exemplo, quantas maneiras diferentes podemos organizar as letras na palavra “BANANA”?
Veja mais sobre Permutações com repetição.
Essas são apenas algumas das técnicas básicas utilizadas na análise combinatória, e elas têm uma ampla gama de aplicações em diversas áreas, como probabilidade, estatística, teoria dos jogos, ciências da computação, entre outras.
Permutações
Permutações são arranjos ordenados de elementos. Em termos simples, uma permutação é uma maneira de organizar ou rearranjar um conjunto de elementos de forma específica.
Por exemplo, considere o conjunto de letras {A, B, C}. Existem várias maneiras diferentes de organizar essas letras:
1. ABC
2. ACB
3. BAC
4. BCA
5. CAB
6. CBA
Cada uma dessas sequências é uma permutação do conjunto {A, B, C}. Note que a ordem das letras importa: “ABC” é uma permutação diferente de “ACB”.
A fórmula para calcular o número de permutações de um conjunto de \( n \) elementos é dada por:
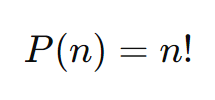
Onde “n!” (lê-se “n fatorial”) representa o produto de todos os inteiros positivos de “1” a “n“. Por exemplo:
- 4! = 4 x 3 x 2 x 1 = 24
Isso significa que há 24 maneiras diferentes de organizar 4 elementos em uma permutação.
Combinações
Combinações são seleções não ordenadas de elementos de um conjunto. Em outras palavras, uma combinação é um subconjunto de elementos escolhidos de um conjunto maior, onde a ordem dos elementos não importa.
Por exemplo, suponha que temos um conjunto de letras {A, B, C}. Se quisermos selecionar duas letras desse conjunto em uma combinação, teríamos as seguintes combinações:
1. {A, B}
2. {A, C}
3. {B, C}
Note que a ordem das letras dentro de cada combinação não importa. Por exemplo, {A, B} é a mesma combinação que {B, A}.
A fórmula para calcular o número de combinações de \( n \) elementos escolhidos \( k \) de cada vez, denotado como C(n, k) é dada por:
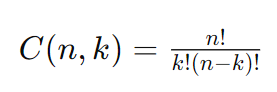
Onde n! representa o fatorial de n, k! representa o fatorial de k, e (n – k)! representa o fatorial de n menos k.
Por exemplo, se quisermos calcular quantas combinações de 3 letras podemos fazer a partir do conjunto {A, B, C, D}, teríamos:
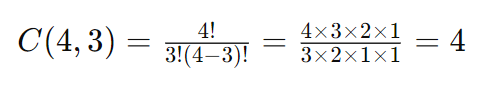
Isso significa que há 4 maneiras diferentes de selecionar um subconjunto de 3 letras do conjunto {A, B, C, D}.
Arranjos
Os arranjos em análise combinatória são como as permutações, mas com uma diferença crucial: eles são arranjos ordenados de elementos, mas com restrições adicionais sobre o número de elementos selecionados ou sobre como eles são organizados.
A fórmula para calcular o número de arranjos de n elementos tomados k de cada vez, denotado como A(n, k) ou nPk, é dada por:
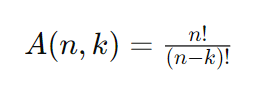
Isso é semelhante à fórmula para permutações, mas com uma diferença. Enquanto nas permutações consideramos todos os elementos, nos arranjos, estamos interessados apenas em uma quantidade específica de elementos, k, dos n elementos disponíveis.
Por exemplo, se tivermos um conjunto de letras {A, B, C, D}, e quisermos calcular o número de arranjos de 3 letras que podemos formar a partir desse conjunto, teríamos:
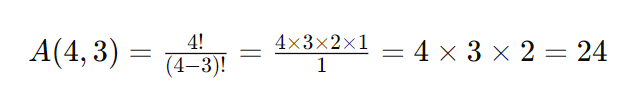
Isso significa que há 24 maneiras diferentes de organizar 3 elementos em um arranjo a partir do conjunto {A, B, C, D}.
Permutações com repetição
Permutações com repetição são um tipo especial de permutação onde alguns dos elementos podem se repetir. Isso significa que, ao organizar os elementos, algumas unidades idênticas são tratadas como se fossem distintas, embora sejam realmente iguais.
A fórmula para calcular o número de permutações com repetição de um conjunto de n elementos, onde n1 elementos são idênticos do tipo 1, n2 elementos são idênticos do tipo 2, e assim por diante até nk elementos idênticos do tipo k, é dada por:
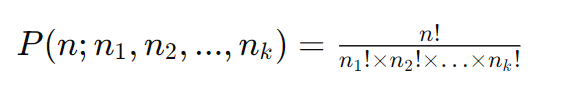
Esta fórmula é uma extensão da fórmula de permutação tradicional. Aqui, n! representa o fatorial de n, e n1!, n2!, …, nk! representam os fatoriais dos números de ocorrências de cada tipo de elemento idêntico.
Por exemplo, considere a palavra “BANANA”. Se quisermos determinar quantas permutações diferentes podemos fazer com essas letras, levando em conta que há duas letras “A” e duas letras “N”, usaríamos a fórmula de permutações com repetição:
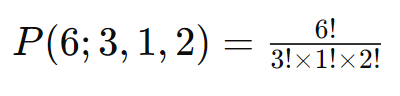
Isso resultaria em 60 permutações diferentes para a palavra “BANANA”.
Como se faz Análise Combinatória?
A análise combinatória pode ser feita utilizando diversas técnicas e métodos, dependendo do problema específico que você está tentando resolver. Aqui estão algumas etapas gerais que você pode seguir ao resolver problemas de análise combinatória:
1. Entenda o problema:
Leia o problema cuidadosamente e certifique-se de entender exatamente o que está sendo perguntado. Identifique os elementos do conjunto e as restrições que podem estar presentes.
2. Escolha a técnica apropriada:
Determine qual técnica de contagem é mais adequada para resolver o problema. Isso pode envolver identificar se é uma questão de permutação, combinação, arranjo ou alguma variação dessas.
3. Conte os casos possíveis:
Liste todas as possíveis combinações, arranjos ou permutações, dependendo da técnica escolhida. Você pode precisar considerar diferentes cenários ou casos específicos.
4. Aplique fórmulas, se necessário:
Se estiver usando fórmulas específicas para permutações, combinações ou arranjos, aplique-as corretamente. Certifique-se de ajustar as fórmulas para levar em conta quaisquer restrições adicionais do problema.
5. Resolva o problema:
Realize os cálculos necessários para determinar o número total de maneiras de organizar, selecionar ou agrupar os elementos conforme solicitado no problema.
6. Verifique sua solução:
Depois de encontrar a resposta, verifique se ela faz sentido em relação ao problema original. Certifique-se de que todas as condições e restrições foram consideradas corretamente.
Essas são etapas gerais que você pode seguir ao resolver problemas de análise combinatória. À medida que você ganha mais prática, você se torna mais habilidoso em identificar a técnica correta a ser aplicada e em resolver os problemas de forma eficiente.
Veja aqui toda a Matéria do ENEM
Veja aqui outros locais para estudar Análise Combinatória: