Porcentagem
A porcentagem é um conceito matemático fundamental que expressa a relação entre uma parte e um todo, representando essa relação como uma fração de 100.
Ela é amplamente utilizada em diversas áreas do conhecimento e do cotidiano, facilitando a compreensão e comparação de proporções de maneira intuitiva.
Seja em contextos financeiros, como a análise de descontos e juros, ou em situações estatísticas, como a distribuição de dados demográficos, a porcentagem oferece uma forma clara e precisa de quantificar e comunicar informações.
Entender como calcular e aplicar porcentagens é essencial para a tomada de decisões informadas e para a resolução de problemas práticos no dia a dia.
O que é porcentagem
A porcentagem é uma medida que expressa uma proporção ou uma relação entre partes de um todo em termos percentuais, ou seja, em partes de 100.
O símbolo “%” é utilizado para representar a porcentagem.
Quando dizemos que algo é, por exemplo, 25% de alguma coisa, isso significa que essa quantidade corresponde a 25 partes de um total de 100 partes.
A palavra “porcentagem” tem origem no latim “per centum”, que significa “por cento” ou “por cada cem”. Portanto, ao lidar com porcentagens, estamos falando sobre uma fração do todo, onde o denominador é sempre 100.
A fórmula básica para calcular a porcentagem de uma quantidade em relação a um todo é:
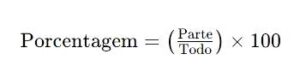
Por exemplo, se você tem 20 maçãs e deseja saber qual é a porcentagem de maçãs vermelhas, sendo que 5 delas são vermelhas, a porcentagem de maçãs vermelhas seria:
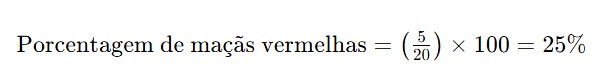
Portanto, 25% das maçãs são vermelhas em relação ao total de maçãs.
Como as porcentagens são representadas?
As porcentagens são geralmente representadas usando o símbolo “%”. Este símbolo é colocado após o valor numérico para indicar a porcentagem da quantidade em relação ao total.
Existem várias maneiras de representar uma porcentagem, dependendo do contexto e do formato desejado. Aqui estão algumas das representações mais comuns de uma porcentagem.
É importante escolher a representação mais adequada ao contexto em que a porcentagem está sendo comunicada. Cada forma de representação tem suas vantagens dependendo do propósito da comunicação e da audiência-alvo.
Aqui estão alguns exemplos de como as porcentagens são representadas:
1. Notação Decimal (percentual):
A porcentagem pode ser representada como um número decimal dividido por 100. Por exemplo, 25% é equivalente a 0,25 em notação decimal.
– 0,25 é representado como 25%.
– 0,75 é representado como 75%.
2. Notação Fracionária:
A porcentagem também pode ser expressa como uma fração com um denominador de 100. Por exemplo, 50% é equivalente a 1/2 em notação fracionária.
– 1/4 é representado como 25%.
– 3/4 é representado como 75%.
3. Notação Decimal com Número Inteiro:
A porcentagem pode ser representada como um número inteiro seguido pelo símbolo “%”. Por exemplo, 75% é uma representação de 75 por cento.
– 1,2 é representado como 120% (pois é equivalente a 1,2 * 100).
4. Notação de Fração com Número Inteiro:
– 3 1/2 é representado como 350% (pois é equivalente a 3 + 1/2 multiplicado por 100).
5. Expressões Verbais:
– Porcentagens podem ser expressas verbalmente, como “um quarto” para 25%, “metade” para 50%, ou “três quartos” para 75%.
– “Metade” é representada como 50%.
– “Um quarto” é representado como 25%.
6. Gráfico de Pizza (ou Gráfico de Setores):
– Em apresentações visuais, uma porcentagem pode ser representada em um gráfico de pizza, onde cada fatia representa uma parte proporcional do todo, e o todo é igual a 100%.
7. Barras de Porcentagem:
– Em gráficos de barras, a altura de uma barra pode representar a porcentagem que ela representa em relação ao todo.
8. Tabela ou Matriz:
– Em tabelas ou matrizes, as porcentagens podem ser apresentadas de forma organizada, mostrando a relação de diferentes partes para o todo.
Como calcular uma porcentagem?
Calcular uma porcentagem envolve determinar qual é a parte de um todo que representa um determinado percentual. Aqui estão os passos básicos para calcular uma porcentagem:
1. Identifique o Todo e a Parte:
- O “Todo” é a quantidade total ou o valor inicial.
- A “Parte” é a quantidade que você está considerando em relação ao todo.
2. Utilize a Fórmula da Porcentagem:
- A fórmula básica para calcular a porcentagem é:
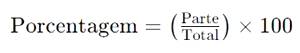
Onde:
- Parte é a quantidade que você quer saber o valor percentual.
- Total é a quantidade total ou o valor base do qual você quer calcular a porcentagem.
3. Substitua os Valores na Fórmula:
- Substitua os valores conhecidos na fórmula. Certifique-se de usar a mesma unidade para “Parte” e “Todo”.
4. Calcule o Resultado:
- Realize as operações matemáticas para encontrar o resultado.
Vamos a alguns exemplos:
Se você tem uma turma de 30 alunos e 12 deles são meninas, a porcentagem de meninas na turma é:
![]()
Se você comprou um produto por R$ 50 e teve um desconto de R$ 10, a porcentagem de desconto é:
![]()
Essa é a abordagem geral para calcular porcentagens.
Lembre-se de que é importante entender claramente o contexto e as unidades envolvidas para garantir que os cálculos sejam precisos.
Como se calcula porcentagem de uma porcentagem?
Calcular a porcentagem de uma porcentagem envolve multiplicar as porcentagens, mas é importante entender que este processo não é tão simples como somar ou subtrair porcentagens.
Vamos abordar isso passo a passo:
Suponhamos que você queira calcular 10% de 20%. Aqui está o processo:
Passo 1: Converta as Porcentagens em Decimais:
- Converta as porcentagens em decimais dividindo-as por 100. Para 10%, isso seria 0,10, e para 20%, seria 0,20.
Passo 2: Multiplique as Porcentagens:
- Multiplique a porcentagem original pelo valor encontrado no Passo 1: 0,10×0,20=0,02
Passo 3: Converta o Resultado de Volta para Porcentagem:
- Se desejar expressar o resultado como uma porcentagem, multiplique o resultado do Passo 2 por 100: 0,02×100=2%
Portanto, 10% de 20% é igual a 2%.
Em resumo, para calcular a porcentagem de uma porcentagem, converta ambas as porcentagens em decimais, multiplique-as e, se necessário, converta o resultado de volta para porcentagem.
Este processo pode ser aplicado a situações mais complexas envolvendo porcentagens de porcentagens. Lembre-se sempre de seguir a ordem correta dos passos para obter resultados precisos.
Leia mais sobre Porcentagens:
Veja aqui toda a Matéria do ENEM
